C:\> Time evolution simulation of the quantum mechanical wavefunction in 3D space

In quantum mechanics, the wave function describes the state of a physical system. In the non-relativistic case, the time evolution of the wave function is described by the time-dependent Schrödinger equation. In 1982, D Kosloff and R Kosloff proposed a method [1] to solve the time-dependent Schrödinger equation efficiently using Fourier transformation. The computational physics research group, led by Géza I. Márk in the Nanotechnology Departement, Institute for Technical Physics and Materials Science, Centre for Energy Research, in collaboration with Belgian researchers developed a simulation method based on three-dimensional wave packet dynamics for the study of the electron dynamics in nanosystems. A simplified, interactive two-dimensional version for educational purposes was published in 2020 [2]. In this work, we demonstrate two improvements of the wave packed dynamical simulation software: (i) the use of GPU, which results in a vast (up to 50x) increase in simulation speed, advanced (ii) the introduction of advanced visualization techniques [3, 4] which are important to correctly interpret huge 4D space-time wave function data sets obtained from the simulation. 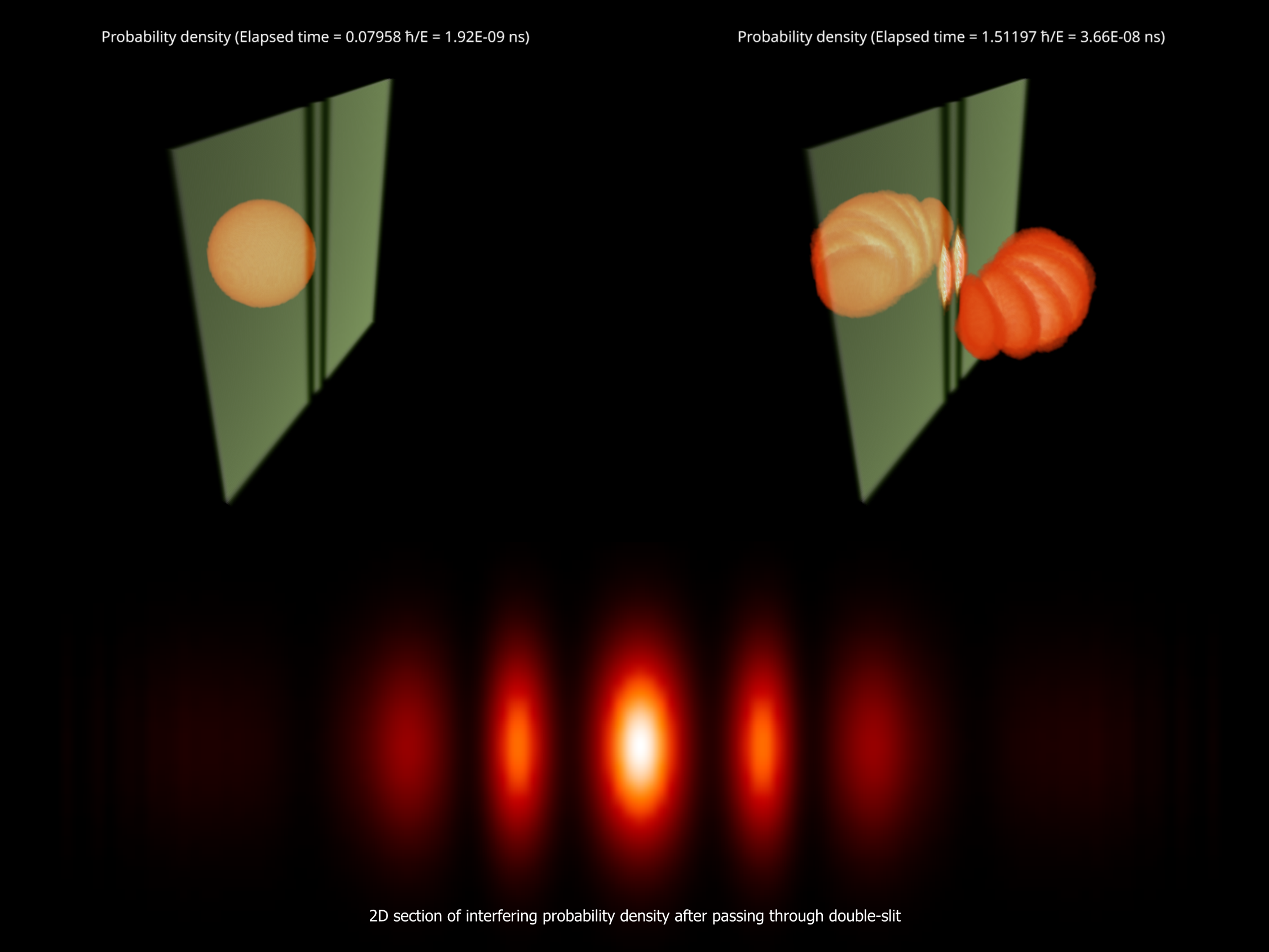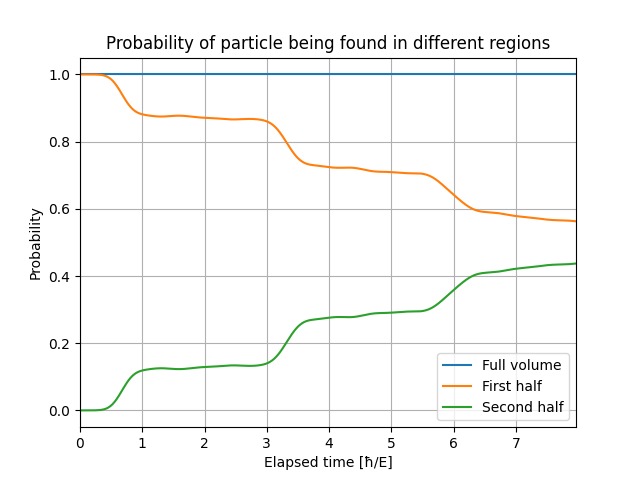We used our implementation to simulate typical quantum phenomena using wave packet dynamics. First, we tried the method on analytically describable cases, such as the simulation of the double-slit experiment, and then we investigated the operation of flash memory. We used raytraced volumetric visualization to render the resulting probability density. In our work, we introduce the basics of wave packet dynamics in quantum mechanics. We describe the used method in detail and showcase our simulation results.

References
[1] Kosloff, D., & Kosloff, R. (1983). A fourier method solution for the time dependent Schrödinger equation as a tool in molecular dynamics. Journal of Computational Physics, 52(1), 35–53. https://doi.org/https://doi.org/10.1016/0021-9991(83)90015-3
[2] Márk, G. I. (2020). Web-Schrödinger: Program for the interactive solution of the time dependent and stationary two dimensional (2D) Schrödinger equation. https://doi.org/10.48550/arXiv.2004.10046
[3] P. Shirley, Ray Tracing in One Weekend, 3rd ed., 2020. [Online]. Available: https://raytracing.github.io/books/RayTracingInOneWeekend.html
[4] B. Csébfalvi, “One step further beyond trilinear interpolation and central differences: Triquadratic reconstruction and its analytic derivatives at the cost of one additional texture fetch,” Computer Graphics Forum, vol. 42, no. 2, pp. 191–200, 2023. [Online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.14753